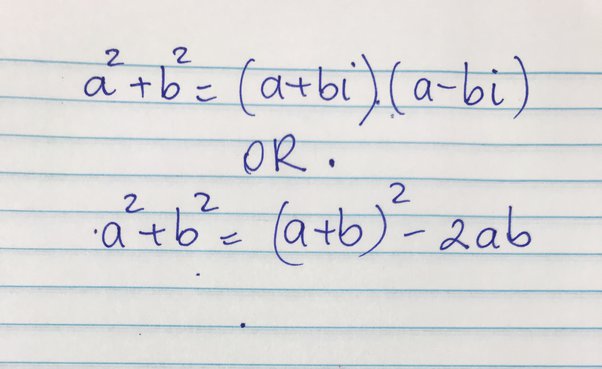Contents
The a2+b2 formula, often referred to as the Pythagorean theorem, stands as a fundamental pillar of mathematics. Its applications reach far and wide, and its significance cannot be overstated. In this article, we will embark on a journey to explore the profound impact of this formula on the world of mathematics, science, and practical problem-solving.
Historical Background a2+b2 Formula
To truly appreciate the a2+b2 formula, we must first delve into its historical roots. This formula finds its origins in ancient Greece, with the brilliant mathematician Pythagoras at its forefront. Pythagoras, who lived between 570 and 495 BC, made groundbreaking contributions to the world of mathematics. His enduring legacy lies in Pythagoras’ Theorem, which forms the basis of the a2+b2 formula.
Over the centuries, the formula has continued to evolve, with various mathematicians contributing to its understanding and applications. Its journey through history has left an indelible mark on the landscape of mathematics, shaping the way we solve problems to this day.
Understanding Pythagoras’ Theorem
At the heart of the a2+b2 formula lies Pythagoras’ Theorem, a concept of timeless importance. This theorem asserts that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. This elegant theorem is succinctly expressed as a2+b2 = c^2, where ‘c’ denotes the length of the hypotenuse.
The beauty of Pythagoras’ Theorem is not confined to its mathematical elegance; it extends to the practical world, where it finds applications in countless scenarios. It provides the foundation for understanding and solving real-world problems involving distance, geometry, and spatial relationships.
Practical Applications
The a2+b2 formula serves as a reliable compass in navigating the complexities of real-world challenges. Its practical applications span diverse fields, making it an invaluable tool for professionals and students alike. Architects harness its power to design structurally sound buildings, ensuring that every corner and angle is accounted for. Engineers rely on it to construct bridges, calculate load-bearing capacities, and design precision machinery. Navigators utilize it for determining distances, both on land and at sea.
In essence, the formula is the key to unlocking solutions to problems that involve spatial relationships and distance measurements. Its applications are as varied as the fields that depend on it, making it an essential concept to master.
Proof and Derivation
To comprehend the formula’s inner workings, it is imperative to understand its proof and derivation. The derivation process is rooted in the principles of geometry and algebra. By isolating ‘c’ and taking the square root of both sides, we arrive at the a2+b2 formula. This process is not just a mathematical exercise; it’s a logical journey that reveals the formula’s inherent truth and reliability.
The relationship between Pythagoras’ Theorem and the formula becomes abundantly clear as one delves into the derivation. This connection serves as the bedrock on which the formula is built, reinforcing its validity and applicability.
Usage in Geometry
In the realm of geometry, the a2+b2 formula is akin to a versatile tool that simplifies complex calculations. Geometry is all about spatial relationships, and this formula excels at helping us make sense of these relationships. It is particularly instrumental in determining angles, distances, and the nature of triangles, specifically right-angled triangles.
For instance, when faced with a problem involving the dimensions of a right-angled triangle, the formula offers a direct route to finding the missing pieces of the puzzle. Its simplicity and accuracy make it a go-to choice for mathematicians, engineers, and anyone dealing with spatial configurations.
Importance in Trigonometry
Beyond geometry, the a2+b2 formula finds a natural home in trigonometry. This branch of mathematics is concerned with the relationships between angles and sides in triangles, and right-angled triangles are of particular interest. The formula’s relevance in trigonometry extends to defining fundamental trigonometric identities, such as the sine and cosine functions.
In trigonometry, the a2+b2 formula plays a pivotal role in establishing these identities and elucidating the connections between angles and sides. It is an essential building block for anyone seeking a profound understanding of trigonometric concepts.
Examples and Illustrations
To make the formula more tangible, let’s embark on a practical journey with examples and vivid illustrations. Imagine a right-angled triangle with one side measuring 3 units and the other measuring 4 units. Using the a2+b2 formula, we can effortlessly calculate the length of the hypotenuse, which turns out to be 5 units. This is a real-world application of the formula, and it showcases its simplicity and precision.
Visual aids, such as diagrams and graphics, further enhance the understanding of the formula’s applicability. They transform abstract mathematical concepts into tangible solutions that we can readily relate to and apply in our daily lives.
Variations and Extensions
The versatility of the a2+b2 formula extends to variations and extensions that find relevance in various mathematical contexts. These variations include a^2 – b^2 and a^2 + 2ab + b^2, each serving a distinct purpose in mathematical problem-solving.
In different scenarios, these variations come into play, offering solutions to problems that may appear insurmountable without them. It’s like having a toolkit of formulas, each tailored to specific challenges and equations.
a2+b2 Formula in 3D Geometry
The formula’s journey doesn’t stop at two-dimensional space; it seamlessly transitions to the realm of three-dimensional geometry. Here, it continues to be an indispensable asset, aiding architects, engineers, and astronomers in their calculations.
In the context of 3D geometry, the formula helps calculate distances between points in space, determine angles, and solve intricate spatial problems. For instance, when designing a complex architectural structure or charting celestial objects in the night sky, this formula is a trusted companion.
Common Mistakes and Pitfalls
As with any mathematical concept, there are potential pitfalls and common errors when working with the a2+b2 formula. It’s crucial to recognize and avoid these pitfalls to ensure the accuracy of calculations.
One common mistake is failing to identify when the formula is applicable. It is specifically designed for right-angled triangles, and using it in other scenarios can lead to erroneous results. Additionally, overlooking the relevance of the formula in a given problem can lead to missed opportunities for elegant solutions.
Exercises and Practice Problems
Learning mathematics is an active endeavor, and to truly master the a2+b2 formula, practice is essential. Here, we provide exercises and practice problems to reinforce your understanding.
Calculate the hypotenuse of a right-angled triangle with sides measuring 6 units and 8 units.
Can you derive the a2+b2 formula from Pythagoras’ Theorem? Try it out and see if you can make the connection between the two.
These exercises serve as opportunities to apply the formula in different scenarios, ensuring that you not only grasp its theory but can also employ it in practical problem-solving.
Advantages of the a2+b2 Formula
The advantages of the a2+b2 formula are manifold. It serves as a versatile tool for simplifying complex spatial calculations and spatial problem-solving. Its elegance lies in its simplicity and accuracy, making it accessible to students and professionals alike.
One of its primary advantages is its wide-ranging applicability. Whether you are an architect, engineer, or mathematician, this formula offers a straightforward method for tackling problems related to spatial relationships. Its efficiency and precision are assets that cannot be overstated.
Limitations and Constraints
While the a2+b2 formula is a powerful mathematical tool, it is not a one-size-fits-all solution. Recognizing its limitations is crucial. The formula is applicable exclusively to right-angled triangles. In scenarios involving other types of triangles, different mathematical methods are necessary to arrive at the correct answers.
Understanding the constraints of the formula is vital for problem-solving. It ensures that you use the right tool for the right job and do not attempt to force its application in unsuitable situations.
Must Read:
Conclusion
In conclusion, the a2+b2 formula, rooted in the enduring principles of Pythagoras’ Theorem, is a mathematical gem with a far-reaching impact. Its historical significance, practical applications, and mathematical elegance combine to make it a fundamental concept in mathematics. Whether you are a student seeking to master the fundamentals of geometry, an engineer designing structures, or an architect creating spaces, this formula is an indispensable companion on your journey.